Labour Market in the Czech Republic
Estimates of confidence intervals | Contents |
Sample surveys are usually connected with sampling and non-sampling errors. The latter are a result, for instance, of administrative drop-outs of dwellings out of the sample, intentional non-response or errors produced by filling in the questionnaire. With these errors, one cannot determine a deviation of estimate without rather wide knowledge of the basic sample. On the other hand, the sampling errors, which arise by applying characteristics of the sample to the basic sample, can be interpreted by means of confidence intervals. The confidence intervals are intervals determined around the estimate in such a way that the actual value of the estimated characteristic falls right within this interval. Constructed most frequently for estimates are the confidence intervals of 95% (by multiplying the respective quantile of the standard normal distribution and the standard deviation) - i.e. an interval, in which the actual value of the estimated characteristic can be found with 95% probability.
The theory of sample surveys distinguishes between the two most frequent type of aggregates: basic aggregates and partial aggregates. The former are some primary aggregates (employment, unemployment, ...) for a basic sample (men, women, persons at working age, men aged 20-24, ...). The latter includes some sub-aggregates in a basic aggregate. For instance, the breakdown of the CZ-NACE in the group of employed persons refers to sub-aggregates. The aggregates by age groups are not sub-aggregates - they are basic aggregates in the population aged 15-19, 20-24, etc.
The confidence intervals in Annex Tables I and II are calculated for the average size of a sample in 2001. For computing the confidence interval of aggregates for other years or quarters and partial aggregates for areas and regions it is necessary to use the following formulas and table III.
a) For the basic aggregate
95% C.I. of estimate Y =
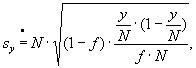
where N is the size of the basic sample
y is the estimate of aggregate Y in the basic sample
f is the respective relative size of sample
b) For the partial aggregate
where N is replaced by the estimate of basic aggregate y and
y is replaced with the partial aggregate yA
the following formula is used:
95% C.I. of partial estimate
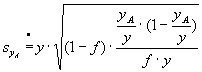
Making the calculations, we should bear in mind that although the aggregates are published in thousands, units should be used in the formula. Both formulas are simplified approximations of precise formulas, but the deviations between the approximations and the precise formulas are not statistically significant. However, the formula for partial aggregates may produce inaccurate results for small estimates of the basic aggregate.
It holds good throughout the publication that aggregates lower than 700 persons are considered to be of very low reliability. This means in practice that their standard deviation is too high or even higher than the estimate itself.
